Stewart platform is a parallel manipulator device for positioning and motion control. It consists of two parallel plates and six adjustable legs for precise adjustment and control of the parallel plates. It is best at providing precise motion with high payloads, which is critical for flight simulators. With its zero latency, low maintenance and clean energy advantages, it is now becoming the preferred solution for precision manufacturing, semiconductor processing and biomedicine.
This article will provide an in-depth introduction to the technical principles, application scenarios and selection strategies of the Stewart platform. We will also explore the many industries that rely on this technology and their importance.
Contents
Overview of Stewart Platform
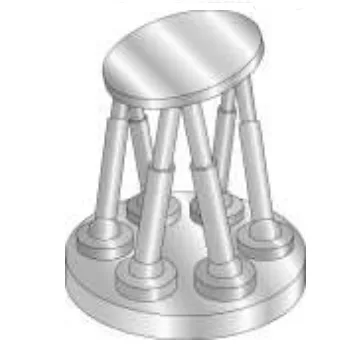
The Stewart platform is also called six-axis positioning platform or 6DOF motion platform, based on parallel kinematics. It has six actuators (electric linear actuators) mounted in pairs at three locations on the platform bottom plate and crossed with three mounting points on the top plate.
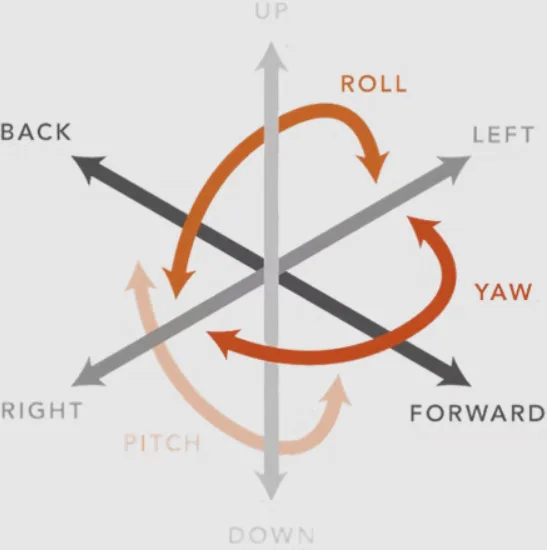
The required position and orientation of the Stewart platform is achieved by combining the lengths of the six legs, converting the six transition degrees of freedom into three positional degrees of freedom and three directional degrees of freedom. It can accurately position Sway (left-right), Surge (front-back) and Heave (up-down) motions as well as three types of rotational motions: pitch, roll and yaw.
Since its invention, the Stewart platform is still used today in flight simulators, military tanks, cars, ships, radio telescopes, and orthopedic surgical robots due to its high positioning accuracy, dynamic efficiency, and payload-to-weight ratio.
The History of Stewart Platform
The Stewart Platform mechanism was originally suggested by Gough in 1947 as a part of a tire-testing machine. He built a prototype of this machine in 1955. In 1965, Stewart suggested the use of such a structure for flight simulators and presented it to academia. Gough was the first to realize the benefits of this mechanism and research in this area was carried out after Stewart’s Paper. Therefore, the combination of Stewart’s and Gough’s design is what is known as the Gough-Stewart Platform or Stewart Platform for short.

From then until 1983 there was little interest for this mechanism. Hunt was one of the first scientists to realize the main advantages of the Stewart platform: high load carrying and precise positioning capability. Since that time, the Stewart platform has been extensively studied and modified looking to improve accuracy, efficiency, increase the workspace, and/or reduce cost.
After 2000, with the breakthrough of high torque density servo motor and planetary roller screw technology, the thrust of electric cylinder increased to more than 50kN, pushing the Stewart platform into the all-electric era.
How the Stewart Platform Works?
The mechanical structure of the Stewart platform adopts a double-layer symmetrical octahedron topology, consisting of a fixed base, a dynamic platform and six servo electric cylinder modules. The base and the dynamic platform are respectively provided with three pairs of hinge points with 120° circular symmetry, which are connected in a 2-2-2 form through six retractable legs (electric cylinders) to form a stable spatial hyperstatic structure. This design feature gives the platform two core advantages:
Ultra-high rigidity: The parallel legs form a closed force chain, which increases the bending stiffness by 5-10 times compared with the serial robot, and the deformation is less than 5μm/m under a dynamic load of 50kN.
Isotropic: The six legs are evenly distributed, which makes the platform have symmetrical mechanical properties in the X/Y/Z axis and rotational degrees of freedom, which is convenient for kinematic decoupling and control parameter setting.
Stewart Platform Structure
Stewart platform design and construction
Stewart platform is a dual-platform structure consisting of an upper and lower platform. The lower platform serves as a base to house and arrange the DC motors in a specific configuration. The upper platform is responsible for transmitting motion to the user and is connected to the lower platform via a connecting rod. The design of these platforms is critical to the overall stability and performance of the motion simulator.
Servo motor and linkage
The servomotors are strategically placed on the lower base platform, taking into account the desired degrees of freedom and motion patterns. The connecting rods (servo cylinders or linear actuators) are carefully designed and positioned to effectively transfer the motor motion to the upper platform.
Control System
The Stewart platform is equipped with a motion control system that can achieve six degrees of freedom. These systems can control the movement of the structure in three translation directions (X, Y, Z axis) and three rotation directions (around X, Y, Z axis). The control system usually consists of sensors, controllers and corresponding software.

Stewart Platform Algorithm
Kinematic Analysis
To move upper plate, each leg must be controlled with an actuator to change the total length of the leg. By controlling each leg’s length independently and with mathematical calculations called forward and inverse kinematics, the location of the top center could be changed precisely. There is no significant error to accumulate with each linkage because it is a distribution of the errors of each individual leg.
For parallel robotic systems typically direct kinematics problem is challenging, but inverse kinematics is straightforward. Forward (direct) kinematics allows the position and orientation of the end effector to be known, given all joint values. Inverse kinematics determines the joint values given a known or desired end-effector position and orientation. The direct kinematics problem of parallel manipulators is by far more challenging than the inverse kinematics problem since it requires solving a set of non-linear equations. Several researchers solved this problem using different methods as presented below.
Analytical solution for the general case is quite difficult due to the nonlinear equation with multiple solutions. A more advantageous technique to solve the direct kinematic problem is the computational one. In this case, in order to find all the real roots, elimination methods are used to simplify the kinematic equations. Although the numerical methods have computational advantages, they are not useful to predict the total number of the roots in the complex domain. P. Dietmaier gave an example of a manipulator with 40 real solutions to the direct kinematics problem. The inverse kinematics Stewart Platform problem has a single solution, but when the number of kinematic chains is reduced, the number of solutions of the inverse kinematics problem increases and the problem becomes more challenging.
There are different approaches to solve the inverse kinematics. One of these approaches was based on a cartesian coordinate system. Another method is using a position vector and a rotation matrix. In a parallel manipulator, the analysis of constraint forces corresponding to the kinematic constraints is very important because the parallel manipulators cannot resist external forces and torques in definite directions due to some constraints. These constraints have to be determined . The architectures limit the motion and behavior of the parallel manipulator platform and generate complex kinematics singularities inside the workspace.
Dynamics Analysis
Several methods of calculation dynamics exist for the Stewart Platform because of its complexity. The most common method found in the literature is the Lagrangian formulation. A less common dynamics method that is known is the Newton-Euler formulation and some implement a Jacobian matrix into this method to help simplify the equations. The Newton-Euler method uses the combination of the Newton equation of motion and Euler angles to calculate the forces acting on the model. Several researchers used this method.
The Lagrangian method for calculating the dynamics of a parallel manipulator is a well-structured set of equations that can be expressed in a closed form. The equations are calculated in symbolic form and are created from calculating the potential and kinetic energies of the manipulator which are then constrained by the geometry and kinematics of the manipulator. Using computational methods in the symbolic form, partial derivatives of the constraining equations and equations of motion can be combined and organized into a system of equations that equal the number of unknowns. Lagrangian multipliers are calculated from the relationship between the active and passive joints of the manipulator. With the Lagrangian multipliers, the forces can be solved for in matrix form from the system of equations mentioned previously.
Applications of the Stewart Platform
The Stewart Platform has revolutionized industries requiring high precision, stability, and dynamic control. Below is a structured overview of its diverse applications, supported by technical insights and real-world implementations.
Aerospace & Flight Simulation
Stewart Platform are foundational in flight simulators for pilot training, replicating realistic flight dynamics such as turbulence, takeoff, and landing. Their ability to simulate 6-DoF motion (pitch, roll, yaw, and translational movements) with sub-millimeter accuracy ensures immersive training environments. For instance, the U.S. Navy employs these platforms to train personnel in maritime operations under simulated wave conditions.
Precision Manufacturing & Machining
In industrial settings, Stewart Platforms excel in high-precision tasks like CNC machining and assembly. Their parallel structure minimizes error accumulation, achieving positioning accuracy as fine as 0.01 mm. A notable example is their integration into multi-tool machining systems, where they enable rapid tool switching without manual intervention, boosting efficiency by 30–40%. The rigidity of the platform also makes it ideal for heavy-load operations in automotive part manufacturing.
Medical Robotics & Surgical Systems
Medical applications leverage the platform’s precision for minimally invasive surgeries and rehabilitation devices. For example, robotic surgical arms use Stewart mechanisms to navigate complex anatomical structures with sub-micron precision, reducing patient trauma. Additionally, platforms like the “Dexterous Eye” assist in ophthalmic surgeries, demonstrating their adaptability in healthcare.
Virtual Reality (VR) & Motion Simulation
Stewart Platforms enhance VR experiences by providing haptic feedback and dynamic motion synchronization. Theme parks and military training facilities use them to simulate driving, space exploration, or combat scenarios. The platform’s low inertia and rapid response enable real-time adjustments, creating lifelike motion effects.
Scientific Research & Metrology
Stewart Platforms enhance VR experiences by providing haptic feedback and dynamic motion synchronization. Theme parks and military training facilities use them to simulate driving, space exploration, or combat scenarios. The platform’s low inertia and rapid response enable real-time adjustments, creating lifelike motion effects.
Space Exploration & Satellite Technology
NASA and ESA utilize Stewart Platforms for satellite docking simulations and antenna positioning. The platform’s stability in microgravity environments ensures precise alignment during space missions. For instance, the HEXAPOD system in the James Webb Space Telescope employs a Stewart-like mechanism for mirror adjustments.
Maritime & Offshore Engineering
Offshore oil rigs and subsea robots rely on Stewart Platforms to stabilize equipment in turbulent waters. Their high load capacity (up to 800 kg) and corrosion-resistant designs make them suitable for deep-sea exploration and pipeline maintenance.
Education & Prototyping
Universities worldwide use Stewart Platforms for robotics courses and research. Open-source projects like ROS-based StewartPlatform-master (C++/MATLAB) allow students to experiment with kinematics and control algorithms, fostering innovation in parallel robotics.
FAQ
Stewart Platform is a 6-degree-of-freedom parallel manipulator composed of a movable top plate connected to a fixed base via six independently adjustable legs. Each leg is typically driven by a linear actuator (e.g., hydraulic or electric) and connected through universal/spherical joints. Its design enables precise control of position and orientation in 3D space
Stewart platforms have applications in flight simulators, machine tool technology, animatronics, crane technology, underwater research, simulation of earthquakes, air-to-sea rescue, mechanical bulls, satellite dish positioning, the Hexapod-Telescope, robotics, and orthopedic surgery.
It is a parallel mechanism that consists of a rigid body top plate, or mobile plate, connected to a fixed base plate and is defined by at least three stationary points on the grounded base connected to six independent kinematic legs.
In the correspondences at the end of this early work, it can be seen that the parallel manipulator now popularly known as the Stewart Platform was first developed by Gough in 1948 for the purpose of testing tires, although the work was not published until 1962
Stewart Platforms have high stiffness and high payload-to-weight ratio due to their parallel structure. Compared with serial robots, they have the advantage of higher positioning accuracy (e.g., micron-level accuracy), and fast response and stability under heavy loads.
A delta robot is a type of parallel robot that consists of three arms connected to universal joints at the base. The key design feature is the use of parallelograms in the arms, which maintains the orientation of the end effector. In contrast, a Stewart platform can change the orientation of its end effector.
The Stewart Platform is a 6-Degrees of Freedom precision parallel robotic positioner system. It is capable of moving in X, Y, Z and Roll, Pitch, Yaw coordinates. What is a Stewart Platform used for? A Stewart Platform is used for positioning its upper or lower plate using its electromechanical actuators.
Dynamic modeling and control system design are often built using MATLAB/Simulink and SimMechanics software. Tools such as Simscape enable physics-based simulation of mechanical interactions (e.g., joint friction, actuator dynamics).
Allcontroller: Customizing the right Stewart platform solution for each customer
To meet the needs of high-precision motion control, you may face complex challenges of multi-axis collaborative control, real-time response and system reliability, which requires expertise in embedded system development and motion control algorithms. To cope with these technical challenges, cooperation with professional motion control solution providers such as Allcontroller has become the preferred strategy in the field of industrial automation.
Allcontroller is an ideal partner for 6DOF parallel control systems, focusing on the research and development and customized services of Stewart platform controllers. The company is headquartered in China, the global manufacturing center, and has more than ten years of technical accumulation in the field of precision motion control. Its team of experts can achieve 0.01 mm positioning accuracy and provide full-stack solutions such as multi-axis servo control, encoder signal processing, and dynamic trajectory planning.
Allcontroller has not only passed ISO 9001 certification, but also built a full life cycle quality control system: from Simulink model simulation verification, hardware-in-the-loop testing (HIL) to on-site vibration and temperature rise detection, to ensure that each Stewart platform controller meets aerospace-grade reliability standards. The combination of customized hardware architecture design (such as compatibility with ISA bus and RS232 interface) and fuzzy ADRC algorithm optimization makes it the preferred technical partner for scenarios such as precision positioning, robot feed cabin adjustment, and simulator drive.
With advanced control technology and rich project experience, we transform your complex posture control requirements into stable and efficient industrial-grade solutions.
Start your Stewart platform project now!




